​小初学的容斥原理和高中必考集合的三种运算有什么关系

小初学的容斥原理和高中必考集合的三种运算有什么关系

容斥‬原理‬其本质是研究集合间的交叉关系，一般在‬小学‬奥数‬或‬初中‬数学‬学到‬，而‬集合‬则‬属于‬高中‬必考内容‬，我们‬初中‬学过‬两个实数除了可以比较大小外，还可以进行加减法运算，如果把集合与实数相类比，我们会想两个集合是否也可以进行“加减”运算呢？我们来研究这个问题。

先来理解集合的运算，其一共包含三种：交集、并集和补集。以下逐一展开：

知识点一：集合的交集

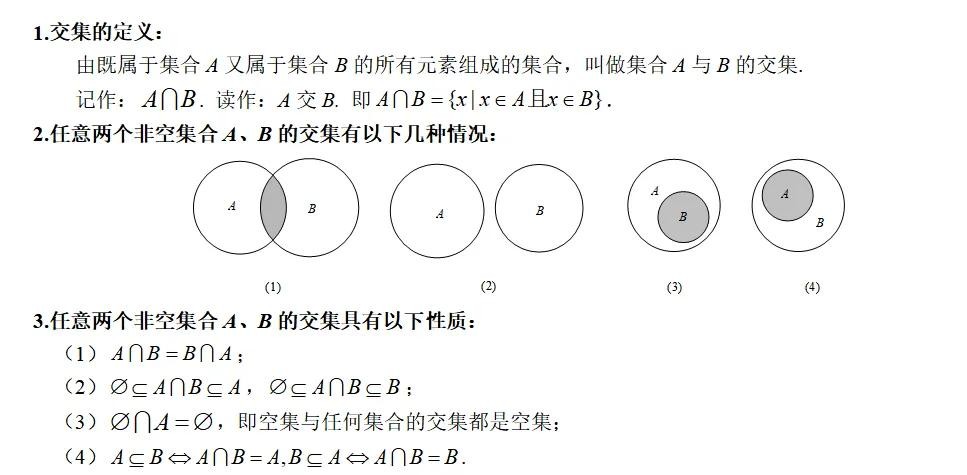
知识点二：集合的并集

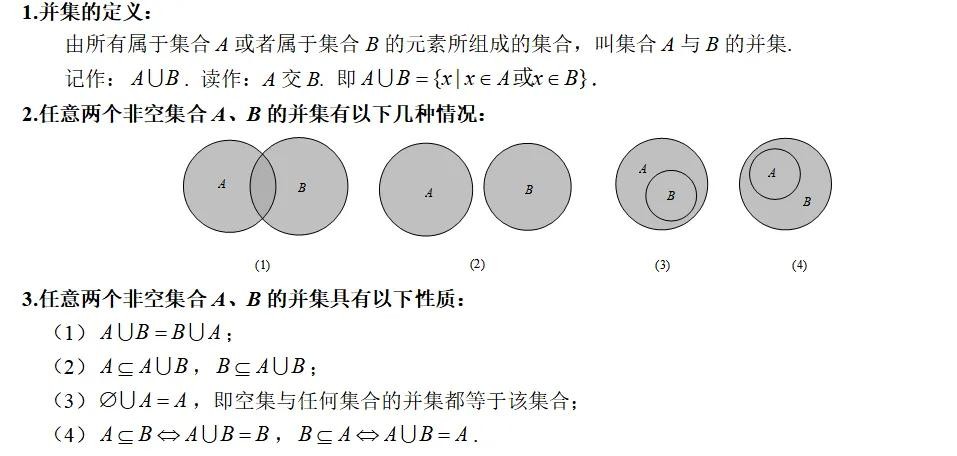
知识点三：集合的补集

知识点四：容斥原理

在计数时，为了没有重复，没有遗漏，使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理.

定义：如果被计数的事物有A、B、C三类，那么，A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数-既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数.（A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C） .

例如：一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？

分析：依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A类元素”，“语文得满分”称为“B类元素”，“语、数都是满分”称为“既是A类又是B类的元素”，“至少有一门得满分的同学”称为“A类和B类元素个数”的总和.为15+12-4=23.

三个集合的容斥关系公式：

|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|

例：分母是1001的最简分数一共有多少个？

分析：这一题实际上就是找分子中不能与1001进行约分的数.由于1001=7×11×13，所以就是找不能被7，11，13整除的数.

解答：1~1001中，有7的倍数1001/7 = 143 （个)；

有11的倍数1001/11 = 91 （个）；有13的倍数1001/13 = 77 （个）；有7*11=77；

77是11的倍数1001/77 = 13 （个），有7*13=91；91是13的倍数；1001/91 = 11 （个），有11*13=143；143是13的倍数1001/143 = 7 （个）.有1001的倍数1个.

由容斥原理知：在1~1001中，能被7或11或13整除的数有（143+91+77）-（13+11+7）+1=281（个），从而不能被7、11或13整除的数有1001-281=720（个）.也就是说，分母为1001的最简分数有720个.

以上供参考。